1. Verifikasie van die fisiese beginsel van die kernformule
Wet van die Behoud van Massa
Alle formules is gebaseer op die fisiese aard van m=ρ×V (massa = digtheid × volume)
Digtheidswaarde
Teoretiese digtheid van suiwer aluminium: 2 698 kg/m³ (20℃)
Die benaderde waarde van 2 700 kg/m³ is redelik vir industriële berekeninge (fout < 0,1%)
2. Verifikasie van die noukeurigheid van meetkundige formules
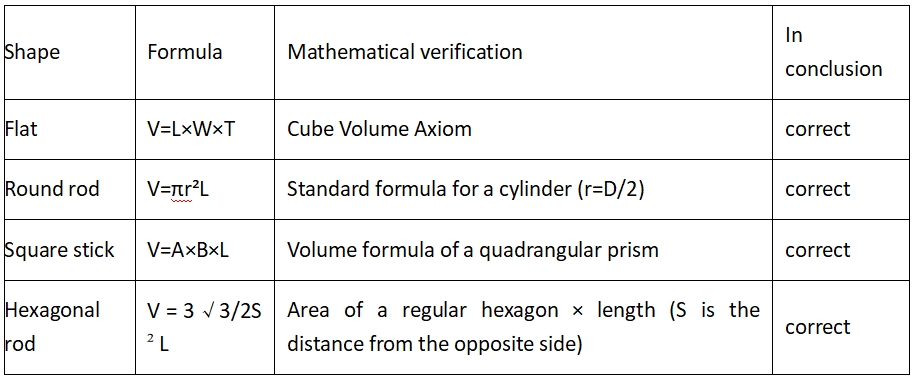
2.1. Standaard geometriese volumeformule
Beperkings vir die formule van die vierkantige buis:
Dit is waar wanneer die buiswanddikte uniform is en die binnehoek 'n regte hoek is (die werklike vierkantige buis het 'n afgeronde oorgang, en die teoretiese fout is ongeveer 1-3%)
3. Verifikasie van Eenheidstelselkonsekwentheid
Kruis-eenheid berekening risikopunt ondersoek
4. Wysiging van Ingenieursgeskiktheid
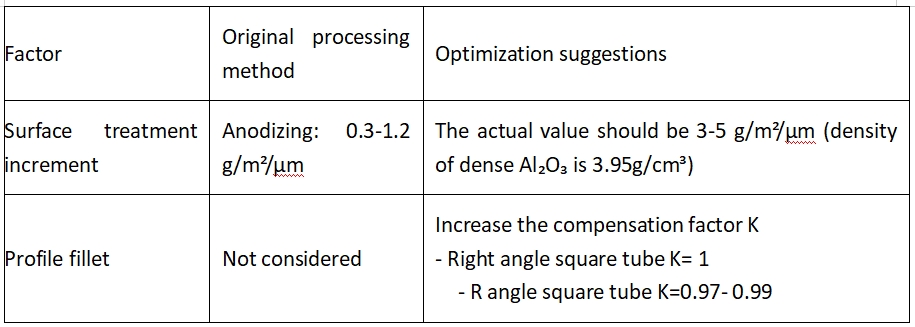
4.1. Kompensasie vir nie-ideale faktore
4.2. Kwantifisering van toleransie-impak
Diktetoleransie ±10% → Gewigsafwyking ±(8% ~ 12%) (dunwandige dele is meer sensitief)
Oplossing: W werklik = W teoreties × (1 + Δt / t) (Δt : dikte-afwyking)
5. Grensvoorwaardetoets
Verifikasie van uiterste gevalle:
Digtheidsanomalie scenario
7xxx-legering (7075): Gemete digtheid 2.810 g/cm³ → Indien 2.7 g/cm³ per abuis gebruik word, is die fout +4.1%.
Formuletabel
4t(A + B) - 4t² is 'n standaard ingenieursberekening wat bereken word deur die omtrek van die profiel met die wanddikte te vermenigvuldig en dan die vier hoeke af te trek.
Berekeningsvoorbeeld:
1.6061 aluminiumplaat(1000 × 500 × 10 mm, lengte 2 m): B = 1000 × 500 × 2 × 0.0027 = 27 kg
2.7075 ronde buis(buitenste deursnee 50 mm, wanddikte 3 mm, lengte 1.5 m): W = [(50-3)×3×3.1416×1.5]×0.00283 ≈ 5.65 kg
3. Vierkantige buis(40×40×2 mm, lengte 3 m): W = [2×2×(40+40-4)×3]×0.0027×0.98 ≈ 2.42 kg
Aanbevole werkvloei
1. Kies digtheid → 2. Meet werklike grootte → 3. Kies kompensasiefaktor → 4. Bereken volgens formule
Plasingstyd: 17 Junie 2025